


БНБ
"БСЭ" (95279)
- Photogallery
- Естественные науки - Математика - Технология
- Авиация и машиностроение
- Высокие технологии
- Вычислительная техника
- Нанотехнология
- Роботехника
- Энергетика
- Электроника
Переменный ток
Определение "Переменный ток" в Большой Советской Энциклопедии
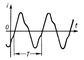 |
| График периодического переменного тока |
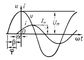 |
| Графики напряжения и тока в цепи переменного тока при сдвиге фазы |
Переменный ток широко применяется в устройствах связи (радио, телевидение, проволочная телефония на дальние расстояния и т. п.).
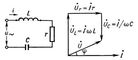 |
| Схема и векторная диаграмма цепи переменного тока с последовательным соединением индуктивности, активного сопротивления и ёмкост |
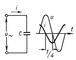 |
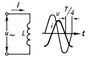
| Схема и графики напряжения и и тока в цепи, содержащей ёмкость |
 |
| Схема и графики напряжения и тока в цепи, содержащей индуктивность |
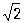 » 0,707 Im, U = Um/
» 0,707 Im, U = Um/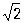 » 0,707 Um. Для синусоидальных токов, удовлетворяющих условию квазистационарности (см. Квазистационарный ток; в дальнейшем будут рассматриваться только такие токи), справедлив Ома закон (закон Ома в дифференциальной форме справедлив и для неквазистационарных токов в линейных цепях). Из-за наличия в цепи Переменный ток индуктивности или (и) ёмкости между током i и напряжением u в общем случае возникает сдвиг фаз j = b - a, зависящий от параметров цепи (активного сопротивления r, индуктивности L, ёмкости С) и угловой частоты w. Вследствие сдвига фаз средняя мощность Р Т. т., измеряемая ваттметром, меньше произведений действующих значений тока и напряжения: Р = IU cosj.
» 0,707 Um. Для синусоидальных токов, удовлетворяющих условию квазистационарности (см. Квазистационарный ток; в дальнейшем будут рассматриваться только такие токи), справедлив Ома закон (закон Ома в дифференциальной форме справедлив и для неквазистационарных токов в линейных цепях). Из-за наличия в цепи Переменный ток индуктивности или (и) ёмкости между током i и напряжением u в общем случае возникает сдвиг фаз j = b - a, зависящий от параметров цепи (активного сопротивления r, индуктивности L, ёмкости С) и угловой частоты w. Вследствие сдвига фаз средняя мощность Р Т. т., измеряемая ваттметром, меньше произведений действующих значений тока и напряжения: Р = IU cosj.
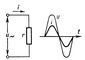 |
| Схема и графики напряжения и тока в цепи, содержащей активное сопротивление |
При наличии в цепи индуктивности L Переменный ток индуцирует в ней эдс самоиндукции eL = - L. di/dt = - wLlm cos (wt + a) = wLIm sin (wt + a - p/2). Эдс самоиндукции противодействует изменениям тока, и в цепи, содержащей только индуктивность, ток отстаёт по фазе от напряжения на четверть периода, то есть j=p/2 (рис. 4). Действующее значение eL равно EL = IwL = IxL, где xL = wL - индуктивное сопротивление цепи. Закон Ома для такой цепи имеет вид: I = U/xL = U/wL.
Когда ёмкость С включена под напряжение u, то её заряд равен q = Cu. Периодические изменения напряжения вызывают периодические изменения заряда, и возникает ёмкостный ток i = dq/dt = C×du/dt = (CUm cos (wt + b) = wCUm sin (wt + b + p/2). Таким образом, синусоидальный Переменный ток, проходящий через ёмкость, опережает по фазе напряжение на её зажимах на четверть периода, то есть j = -p/2 (рис. 5). Эффективные значения в такой цепи связаны соотношением I = wCU = U/xc, где xc = 1/wС - ёмкостное сопротивление цепи.
Если цепь Переменный ток состоит из последовательно соединённых r, L и С, то её полное сопротивление равно 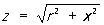 , где x = xL - xc = wL - 1/wC - реактивное сопротивление цепи Переменный ток Соответственно, закон Ома имеет вид:
, где x = xL - xc = wL - 1/wC - реактивное сопротивление цепи Переменный ток Соответственно, закон Ома имеет вид: 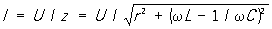 , а сдвиг фаз между током и напряжением определяется отношением реактивного сопротивления цепи к активному: tgj = х/r. В такой цепи при совпадении частоты w вынужденных колебаний, создаваемых источником Переменный ток, с резонансной частотой w0 = 1/
, а сдвиг фаз между током и напряжением определяется отношением реактивного сопротивления цепи к активному: tgj = х/r. В такой цепи при совпадении частоты w вынужденных колебаний, создаваемых источником Переменный ток, с резонансной частотой w0 = 1/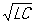 индуктивное и ёмкостное сопротивления равны (wL = 1/wС) и полностью компенсируют друг друга, сила тока максимальна и наблюдается явление резонанса (см. Колебательный контур). В условиях резонанса напряжения на индуктивности и ёмкости могут значительно (часто во много раз) превышать напряжение на зажимах цепи.
индуктивное и ёмкостное сопротивления равны (wL = 1/wС) и полностью компенсируют друг друга, сила тока максимальна и наблюдается явление резонанса (см. Колебательный контур). В условиях резонанса напряжения на индуктивности и ёмкости могут значительно (часто во много раз) превышать напряжение на зажимах цепи.
Облегчение расчётов цепей синусоидальных Переменный ток достигается построением так называемых векторных диаграмм. Векторы синусоидальных тока и напряжения принято помечать точкой над буквенным обозначением (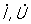 ). Длины векторов обычно берутся равными (в масштабе построения диаграммы) действующим значениям I и U, а углы между векторами - равными сдвигам фаз между мгновенными значениями соответствующих величин. Алгебраическому сложению мгновенных значений синусоидальных величин одной и той же частоты соответствует геометрическое сложение векторов этих величин. На рис. 6 показана векторная диаграмма для цепи Переменный ток с последовательно соединёнными r, L, С. Мгновенное значение напряжения на зажимах этой цепи равно алгебраической сумме напряжений на активном и реактивном сопротивлениях: u = uL + ur + uc, следовательно,
). Длины векторов обычно берутся равными (в масштабе построения диаграммы) действующим значениям I и U, а углы между векторами - равными сдвигам фаз между мгновенными значениями соответствующих величин. Алгебраическому сложению мгновенных значений синусоидальных величин одной и той же частоты соответствует геометрическое сложение векторов этих величин. На рис. 6 показана векторная диаграмма для цепи Переменный ток с последовательно соединёнными r, L, С. Мгновенное значение напряжения на зажимах этой цепи равно алгебраической сумме напряжений на активном и реактивном сопротивлениях: u = uL + ur + uc, следовательно, 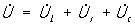 . При построении диаграммы исходным служит вектор тока, так как во всех участках неразветвлённой цепи ток один и тот же. Поскольку индуктивное напряжение опережает по фазе ток на p/2, а ёмкостное отстаёт от тока на p/2 (то есть они находятся в противофазе), при последовательном соединении они друг друга частично компенсируют.
. При построении диаграммы исходным служит вектор тока, так как во всех участках неразветвлённой цепи ток один и тот же. Поскольку индуктивное напряжение опережает по фазе ток на p/2, а ёмкостное отстаёт от тока на p/2 (то есть они находятся в противофазе), при последовательном соединении они друг друга частично компенсируют.
Векторные диаграммы наглядно иллюстрируют ход вычислений и служат для контроля над ними; построенные с соблюдением масштаба, они позволяют графически определить эффективное напряжение U в цепи и угол сдвига фаз j.
Для расчётов разветвленных цепей квазистационарного Переменный ток используют Кирхгофа правила. При этом обычно применяют метод комплексных величин (символический метод), который позволяет выразить в алгебраической форме геометрические операции с векторами Переменный ток и применить, таким образом, для расчётов цепей Переменный ток все методы расчётов цепей постоянного тока.
Несинусоидальность Переменный ток в электроэнергетических системах обычно нежелательна, и принимаются специальные меры для её подавления. Но в цепях электросвязи, в полупроводниковых и электронных устройствах несинусоидальность создаётся самим рабочим процессом. Если среднее за период значение тока не равно нулю, то он содержит постоянную составляющую. Для анализа процессов в цепях несинусоидального тока его представляют в виде суммы простых гармонических составляющих, частоты которых равны целым кратным числам основной частоты: I = i0 + I1m sin (wt + a1)+ I2m sin (2wt + a2) +... + lkm sin (kwt + ak). Здесь I0 - постоянная составляющая тока, Iimsin (wt + a1) - первая гармоническая составляющая (основная гармоника), остальные члены - высшие гармоники. Расчёт линейных цепей несинусоидального тока на основании принципа суперпозиции (наложения) ведётся для каждой составляющей (так как xL и xc зависят от частоты). Алгебраическое сложение результатов таких расчётов даёт мгновенное значение силы (или напряжения) несинусондального тока.
Лит.: Теоретические основы электротехники, 3 изд., ч. 2, М., 1970; Нейман Л. Р., Демирчан К. С., Теоретические основы электротехники, т. 1-2, М.- Л., 1966; Касаткин А. С., Электротехника, 3 изд., М., 1974; Поливанов К. М., Линейные электрические цепи с сосредоточенными постоянными, М., 1972 (Теоретические основы электротехники, т. 1).
А. С. Касаткин.
| "БСЭ" >> "П" >> "ПЕ" >> "ПЕР" >> "ПЕРЕ" |
Статья про "Переменный ток" в Большой Советской Энциклопедии была прочитана 1242 раз
| Жаренный морской черенок |
| Жаренный морской черенок |
TOP 20
- Лемке Михаил Константинович
- Сульфгидрильные группы
- «Казарменный коммунизм»
- Японское море
- Периодическая система элементов
- Глициния
- Башкирская Автономная Советская Социалистическая Республика
- Иммунитет (историч.)
- Андаманское море
- Сенсуализм
- Объединённая партия гаитянских коммунистов
- «Сообразительный»
- Балкано-кавказская раса
- Навигация (морск.)
- Звёздная астрономия
- Ямполь (пос. гор. типа в Донецкой обл.)
- Мандельштама - Бриллюэна рассеяние
- Кульчицкая Елена Львовна
- Театральные учебные заведения
- Электрическая постоянная