


БНБ
"БСЭ" (95279)
- Photogallery
- Естественные науки - Математика - Технология
- Авиация и машиностроение
- Высокие технологии
- Вычислительная техника
- Нанотехнология
- Роботехника
- Энергетика
- Электроника
Поверхность
Определение "Поверхность" в Большой Советской Энциклопедии
Поверхность, одно из основных геометрических понятий. При логическом уточнении этого понятия в разных отделах геометрии ему придаётся различный смысл.
1) В школьном курсе геометрии рассматриваются плоскости, многогранники, а также некоторые кривые поверхности. Каждая из кривых Поверхность определяется специальным способом, чаще всего как множество точек, удовлетворяющих некоторым условиям. Например, Поверхность шара — множество точек, отстоящих на заданном расстоянии от данной точки. Понятие «Поверхность» лишь поясняется, а не определяется. Например, говорят, что Поверхность есть граница тела или след движущейся линии.
2) Математически строгое определение Поверхность основывается на понятиях топологии. При этом основным является понятие простой поверхности, которую можно представить как кусок плоскости, подвергнутый непрерывным деформациям (растяжениям, сжатиям и изгибаниям). Более точно, простой Поверхность называется образ гомеоморфного отображения (т. е. взаимно однозначного и взаимно непрерывного отображения) внутренности квадрата (см. Гомеоморфизм). Этому определению можно дать аналитическое выражение. Пусть на плоскости с прямоугольной системой координат u и u задан квадрат, координаты внутренних точек которого удовлетворяют неравенствам 0 < u < 1, 0 < u < 1. Гомеоморфный образ квадрата в пространстве с прямоугольной системой координат х, у, z задаётся при помощи формул х = j(u, u), у = Y(u, u), z = c(u, u) (параметрические уравнения Поверхность). При этом от функций j(u, u), Y(u, u) и c(u, u) требуется, чтобы они были непрерывными и чтобы для различных точек (u, u) и (u’, u’) были различными соответствующие точки (x, у, z) и (x’, у’, z"). Примером простой Поверхность является полусфера. Вся же сфера не является простой Поверхность Это вызывает необходимость дальнейшего обобщения понятия Поверхность Поверхность, окрестность каждой точки которой есть простая Поверхность, называется правильной. С точки зрения топологического строения, Поверхность как двумерные многообразия разделяются на несколько типов: замкнутые и открытые, ориентируемые и неориентируемые и т.д. (см. Многообразие).
В дифференциальной геометрии исследуемые Поверхность обычно подчинены условиям, связанным с возможностью применения методов дифференциального исчисления. Как правило, это — условия гладкости Поверхность, т. е. существования в каждой точке Поверхность определённой касательной плоскости, кривизны и т.д. Эти требования сводятся к тому, что функции j(u, u), Y(u, u), c(u, u) предполагаются однократно, дважды, трижды, а в некоторых вопросах — неограниченное число раз дифференцируемыми или даже аналитическими функциями. Кроме того, требуется, чтобы в каждой точке хотя бы один из определителей ,
, 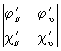 ,
, 
был отличен от нуля (см. Поверхностей теория).
В аналитической геометрии и в алгебраической геометрии Поверхность определяется как множество точек, координаты которых удовлетворяют определённому виду уравнений:
Ф (х, у, z) = 0. (*)
Таким образом, определённая Поверхность может и не иметь наглядного геометрического образа. В этом случае для сохранения общности говорят о мнимых Поверхность Например, уравнение
х2 + у2 + z2 + 1 = 0
определяет мнимую сферу, хотя в действительном пространстве нет ни одной точки, координаты которой удовлетворяют такому уравнению (см. также Поверхности второго порядка). Если функция Ф (х, у, z) непрерывна в некоторой точке и имеет в ней непрерывные частные производные  , из которых хотя бы одна не обращается в нуль, то в окрестности этой точки Поверхность, заданная уравнением (*), будет правильной Поверхность
, из которых хотя бы одна не обращается в нуль, то в окрестности этой точки Поверхность, заданная уравнением (*), будет правильной Поверхность
| "БСЭ" >> "П" >> "ПО" >> "ПОВ" |
Статья про "Поверхность" в Большой Советской Энциклопедии была прочитана 709 раз
| Коптим скумбрию в коробке |
| Каша со столетними яйцами |
TOP 20
- Лемке Михаил Константинович
- Сульфгидрильные группы
- «Казарменный коммунизм»
- Японское море
- Периодическая система элементов
- Глициния
- Башкирская Автономная Советская Социалистическая Республика
- Иммунитет (историч.)
- Объединённая партия гаитянских коммунистов
- Андаманское море
- Сенсуализм
- «Сообразительный»
- Балкано-кавказская раса
- Навигация (морск.)
- Звёздная астрономия
- Ямполь (пос. гор. типа в Донецкой обл.)
- Мандельштама - Бриллюэна рассеяние
- Кульчицкая Елена Львовна
- Театральные учебные заведения
- Электрическая постоянная