Многообразие

Определение "Многообразие" в Большой Советской Энциклопедии

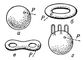Замкнутые двумерные многообразия

Многообразие, математическое понятие, уточняющее и обобщающее на любое число измерений понятия линии и поверхности, не содержащих особых точек (т. e. линии без точек самопересечения, концевых точек и т. п. и поверхности без самопересечений, краев и т. п.).

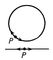Одномерные многообразия

Примером одномерного Многообразие могут служить прямая, парабола, окружность, эллипс, вообще любая линия, у каждой точки которой существует окрестность, являющаяся взаимно однозначным и непрерывным (или, как говорят в топологии, гомеоморфным) образом интервала (внутренней части отрезка прямой). Интервал сам является одномерным Многообразие, отрезок же не является Многообразие (так как концы его не имеют окрестностей указанного вида).

Примером двумерного Многообразие может служить любая область на плоскости (например, внутренность круга x² + y² < r²), сама плоскость, параболоид, сфера, эллипсоид, тор и т. п. Двумерные Многообразие характеризуются тем, что у каждой их точки имеется окрестность, гомеоморфная внутренности круга. Это требование исключает, например, из числа двумерных Многообразие коническую поверхность (её вершина, в которой сходятся две её полости, не имеет требуемого вида окрестности). Однако выделяют специальный класс объектов, которые не удовлетворяют этому требованию, - т. н. многообразия с краем (например, замкнутый круг x² + y² £ r²).

Примером трёхмерного Многообразие может служить обычное евклидово пространство, а также любое открытое множество в евклидовом пространстве. Трёхмерные Многообразие характеризуются тем, что у каждой их точки имеется окрестность, гомеоморфная внутренности шара.

Многообразие разделяются на замкнутые и открытые (определение см. ниже). В случае одного измерения каждое замкнутое Многообразие гомеоморфно окружности, а каждое открытое - прямой (на рис. 1 изображены одномерные Многообразие и окрестности точки Р на каждом из них). В случае двух измерений уже замкнутые Многообразие довольно разнообразны. Они распадаются на бесконечное число топологических типов: сфера - поверхность рода 0 (рис. 2, а), тор - поверхность рода 1 (рис. 2, б), «крендель» - поверхность рода 2 (рис. 2, в), вообще «сфера с n ручками» - поверхность рода n (на рис. 2, г изображена такая поверхность при n = 3). Этими примерами исчерпываются все топологические типы замкнутых двумерных ориентируемых Многообразие (см. также Ориентируемая поверхность). Существует ещё бесконечное число замкнутых двумерных неориентируемых Многообразие - односторонних поверхностей, например проективная плоскость, т. н. односторонний тор (Клейна поверхность). Имеется и классификация открытых двумерных Многообразие Полная классификация Многообразие трёх измерений не найдена (1974) (даже для случая замкнутых Многообразие).

Многообразием n измерений (или n-мерным многообразием) называется всякое хаусдорфово топологическое пространство, обладающее следующим свойством: каждая его точка имеет окрестность, гомеоморфную внутренности n-мерного шара, и всё пространство может быть представлено в виде суммы конечного или бесконечного (счётного) множества таких окрестностей. Многообразие называется замкнутым, если оно компактно (см. Компактность), в противном случае - открытым. Иногда к определению Многообразие прибавляют ещё требование его связности: каждые две точки Многообразие могут быть в нём соединены непрерывной дугой.

Введение в математику понятия Многообразие любого (натурального) числа измерений n было вызвано весьма разнообразными потребностями геометрии, математического анализа, механики и физики. Важность достаточной широты понимания Многообразие как топологического пространства основана на том, что точками так определённых Многообразие могут быть объекты любой природы, например прямые, сферы, матрицы и т. д.

При надлежащем добавлении требований к определению Многообразие устанавливается понятие гладкого, или дифференцируемого, многообразия. На гладком Многообразие имеется возможность рассматривать дифференцируемые функции и дифференцируемые отображения в себя или в другие гладкие Многообразие Гладкие Многообразие имеют особенно большое значение в современной математике, поскольку именно они наиболее широко используются в приложениях и смежных областях (например, конфигурационные пространства и фазовые пространства в механике и физике). На гладких Многообразие можно ввести метрику, превратив его в риманово пространство. Это позволяет строить дифференциальную геометрию на Многообразие Например, введя некоторым образом метрику в конфигурационном пространстве механической системы, можно истолковать траектории движения как геодезические линии в этом пространстве (см. Наименьшего действия принцип). Многообразие, для элементов которого определено (дифференцируемое) умножение, превращающее Многообразие в группу, называется группой Ли (см. Непрерывная группа).

  Понятие Многообразие играет большую роль в теории алгебраических функций, непрерывных групп и т. д. Во всех этих приложениях существенны свойства Многообразие, не изменяющиеся при топологических преобразованиях, - т. н. топологические свойства. К ним относятся, например, ориентируемость или неориентируемость Многообразие (см. Ориентация). Изучение этих свойств является одной из важнейших задач топологии.

Лит.: Александров П. С. и Ефремович В. А., Очерк основных понятий топологии, Многообразие - Л., 1936; Александров П. С., Комбинаторная топология, Многообразие - Л., 1947; Ленг С., Введение в теорию дифференцируемых многообразий, пер. с англ., Многообразие, 1967.
  Н. В. Ефимов.