


БНБ
"БСЭ" (95279)
- Photogallery
- Естественные науки - Математика - Технология
- Авиация и машиностроение
- Высокие технологии
- Вычислительная техника
- Нанотехнология
- Роботехника
- Энергетика
- Электроника
Самосопряжённый оператор
Определение "Самосопряжённый оператор" в Большой Советской Энциклопедии
Самосопряжённый оператор оператор, совпадающий со своим сопряжённым (см. Сопряжённые операторы). иначе называется эрмитовым. Теория Самосопряжённый оператор возникла как обобщение теории интегральных уравнений с симметричным ядром, самосопряжённых дифференциальных уравнений, симметрических матриц и т. д. Примерами Самосопряжённый оператор могут служить оператор умножения на независимое переменное в пространстве функций, заданных на всей числовой прямой и имеющих интегрируемый квадрат, оператор дифференцирования 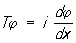 в том же пространстве и т. д.
в том же пространстве и т. д.
Если функция К (х, у) непрерывна на квадрате а £ х £ b, а £ у £ b и К (х, у) = К (у, х), то интегральный оператор 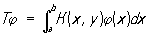 самосопряжён. Спектр Самосопряжённый оператор (см. Спектр оператора) лежит на действительной оси. В квантовой механике физическим величинам соответствуют Самосопряжённый оператор, спектр которых даёт возможные значения этих величин. Самосопряжённый оператор может быть в известном смысле представлен в виде интеграла, являющегося пределом линейных комбинаций попарно ортогональных проекционных операторов с действительными коэффициентами. См. Спектральный анализ линейных операторов, Операторов теория.
самосопряжён. Спектр Самосопряжённый оператор (см. Спектр оператора) лежит на действительной оси. В квантовой механике физическим величинам соответствуют Самосопряжённый оператор, спектр которых даёт возможные значения этих величин. Самосопряжённый оператор может быть в известном смысле представлен в виде интеграла, являющегося пределом линейных комбинаций попарно ортогональных проекционных операторов с действительными коэффициентами. См. Спектральный анализ линейных операторов, Операторов теория.
| "БСЭ" >> "С" >> "СА" >> "САМ" >> "САМО" |
Статья про "Самосопряжённый оператор" в Большой Советской Энциклопедии была прочитана 476 раз
| Бургер двойного помола |
| Английская картошка фри |
TOP 20
- Лемке Михаил Константинович
- Сульфгидрильные группы
- «Казарменный коммунизм»
- Глициния
- Японское море
- Периодическая система элементов
- Башкирская Автономная Советская Социалистическая Республика
- Иммунитет (историч.)
- Андаманское море
- Сенсуализм
- «Сообразительный»
- Звёздная астрономия
- Балкано-кавказская раса
- Ямполь (пос. гор. типа в Донецкой обл.)
- Навигация (морск.)
- Кульчицкая Елена Львовна
- Мандельштама - Бриллюэна рассеяние
- Театральные учебные заведения
- Электрическая постоянная
- Энсор Джеймс