


БНБ
"БСЭ" (95279)
- Photogallery
- Естественные науки - Математика - Технология
- Авиация и машиностроение
- Высокие технологии
- Вычислительная техника
- Нанотехнология
- Роботехника
- Энергетика
- Электроника
Фонон
Определение "Фонон" в Большой Советской Энциклопедии
Фонон (от греч. phone – звук), квант колебательного движения атомов кристалла. Колебания атомов кристалла благодаря взаимодействию между ними распространяются по кристаллу в виде волн, каждую из которых можно охарактеризовать квазиволновым вектором k и частотой w, зависящей от k: w = wn(k), где индекс n = 1,2,..., 3 r (r – число атомов в элементарной ячейке кристалла) обозначает тип колебания (см. Колебания кристаллической решётки). Согласно законам квантовой механики, колебательная энергия атомов кристалла может принимать значения, равные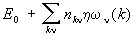 , где E0 – энергия основного состояния,
, где E0 – энергия основного состояния, 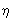 – Планка постоянная. Каждой волне можно поставить в соответствие квазичастицу – Фонон Энергия Фонон равна:
– Планка постоянная. Каждой волне можно поставить в соответствие квазичастицу – Фонон Энергия Фонон равна:  , квазиимпульс р =
, квазиимпульс р =  k. Число nкn следует трактовать как число Фонон Различают акустический и оптический Фонон; для акустического Фонон при р ® 0 E = sp, где s – скорость звука; для оптического Фонон при р ® 0 Emin ¹ 0 (у простых кристаллов с r = 1 оптического Фонон нет).
k. Число nкn следует трактовать как число Фонон Различают акустический и оптический Фонон; для акустического Фонон при р ® 0 E = sp, где s – скорость звука; для оптического Фонон при р ® 0 Emin ¹ 0 (у простых кристаллов с r = 1 оптического Фонон нет).
Фонон взаимодействуют друг с другом, с др. квазичастицами (электронами проводимости, магнонами и др.) и со статическими дефектами кристалла (с вакансиями, дислокациями, с границами кристаллитов, поверхностью образца, с чужеродными включениями). При столкновениях Фонон выполняются законы сохранения энергии и квазиимпульса. Последний является более общим, чем закон сохранения импульса (см. Сохранения законы), т.к. суммарный квазиимпульс сталкивающихся квазичастиц, в частности Фонон, может изменяться на величину 2p b, где b – вектор обратной решётки. Такие столкновения называются процессами переброса, в отличие от нормальных столкновений (b = 0). Возможность процесса переброса – следствие периодичности в расположении атомов кристалла.
b, где b – вектор обратной решётки. Такие столкновения называются процессами переброса, в отличие от нормальных столкновений (b = 0). Возможность процесса переброса – следствие периодичности в расположении атомов кристалла.
Среднее число Фонон  определяется формулой Планка:
определяется формулой Планка:
где T – температура, k – Больцмана постоянная. Эта формула совпадает с распределением частиц газа, подчиняющихся статистике Бозе – Эйнштейна, когда химический потенциал равен нулю (см. Статистическая физика). Равенство нулю химического потенциала означает, что число Nф > Фонон в кристалле не сохраняется, а зависит от температуры. Для всех твёрдых тел Nф ~ T3 при Т ® 0 и Nф ~ Т при Т >> Qд (Qд – Дебая температура). Понятие Фонон позволяет описать тепловые и др. свойства кристаллов, используя методы кинетической теории газов. Фонон в большинстве случаев представляют собой главный тепловой резервуар твёрдого тела. Теплоёмкость кристаллического твёрдого тела практически совпадает с теплоёмкостью газа Фонон Теплопроводность кристалла можно описать как теплопроводность газа Фонон, теплосопротивление которого обеспечивается процессами переброса.
Рассеяние электронов проводимости при взаимодействии с Фонон – основной механизм электросопротивления металлов и полупроводников. Способность электронов проводимости излучать и поглощать Фонон приводит к притяжению электронов друг к другу, что при низких температурах является причиной перехода ряда металлов в сверхпроводящее состояние (см. Сверхпроводимость, Купера эффект). Излучение Фонон возбуждёнными атомами и молекулами тел обеспечивает возможность безызлучательных электронных переходов (см. Релаксация). В релаксационных процессах в твёрдых телах Фонон обычно служат стоком для энергии, запасённой др. степенями свободы кристалла, например электронными.
Среднюю энергию газа Фонон (как и др. квазичастиц) можно характеризовать величиной, подобной температуре обычного газа. Однако благодаря сравнительно слабой связи Фонон с др. квазичастицами фононная (или решёточная) температура может отличаться от температуры др. квазичастиц (электронов проводимости, магнонов, экситонов). В аморфных (стеклообразных) телах понятие Фонон удаётся ввести только для длинноволновых акустических колебаний, мало чувствительных к взаимному расположению атомов.
Фонон называются также элементарные возбуждения в сверхтекучем гелии, описывающие колебательное движение квантовой жидкости (см. Сверхтекучесть).
Лит.: Займан Дж., Электроны и фононы, пер. с англ., М., 1962; Косевич А. М., Основы механики кристаллической решетки, М., 1972; Рейсленд Дж., Физика фононов, пер. с англ., М., 1975.
М. И. Каганов.
| "БСЭ" >> "Ф" >> "ФО" >> "ФОН" |
Статья про "Фонон" в Большой Советской Энциклопедии была прочитана 1558 раз
| Коптим скумбрию в коробке |
| Английское куриное карри |
TOP 20
- Лемке Михаил Константинович
- Сульфгидрильные группы
- «Казарменный коммунизм»
- Японское море
- Периодическая система элементов
- Глициния
- Башкирская Автономная Советская Социалистическая Республика
- Иммунитет (историч.)
- Андаманское море
- Сенсуализм
- «Сообразительный»
- Балкано-кавказская раса
- Навигация (морск.)
- Звёздная астрономия
- Ямполь (пос. гор. типа в Донецкой обл.)
- Кульчицкая Елена Львовна
- Мандельштама - Бриллюэна рассеяние
- Театральные учебные заведения
- Электрическая постоянная
- Энсор Джеймс