


БНБ
"БСЭ" (95279)
- Photogallery
- Естественные науки - Математика - Технология
- Авиация и машиностроение
- Высокие технологии
- Вычислительная техника
- Нанотехнология
- Роботехника
- Энергетика
- Электроника
Гаусса формулы
Определение "Гаусса формулы" в Большой Советской Энциклопедии
Гаусса формулы, формулы, относящиеся к различным разделам математики и носящие имя К. Гаусса.
1) Квадратурные Гаусса формулы — формулы вида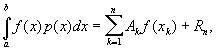
в которых узлы xk и коэффициенты Ak не зависят от функции f (x) и выбраны так, что формула точна (т. е. Rn = 0) для произвольного многочлена степени 2n - 1. В отличие от квадратурных формул Ньютона — Котеса, узлы в квадратурных Гаусса формулы, вообще говоря, не являются равноотстоящими. Если р (х) ³ 0 и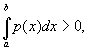
то для любого натурального n имеется единственная квадратурная Гаусса формулы Эти формулы имеют большое практическое значение, т.к. в ряде случаев они дают значительно большую точность, чем квадратурные формулы с тем же числом равноотстоящих узлов. Сам Гаусс исследовал (1816) случай р (х) º 1.
2) Гаусса формулы, выражающая полную кривизну К поверхности через коэффициенты её линейного элемента; в координатах, для которых ds2 = l(du2 + dv2), Гаусса формулы имеет вид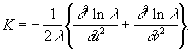
Эта формула была опубликована в 1827 и показывает, что полная кривизна не меняется при изгибании поверхности. Она составляет содержание одного из основных предложений созданной Гауссом внутренней геометрии поверхности.
3) Гаусса формулы для сумм Гаусса: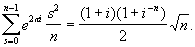
Эта формула была использована Гауссом (1801) в одном из доказательств закона взаимности квадратичных вычетов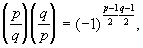
где р и q — нечётные простые числа, а 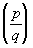 — Лежандра символ. Она явилась первым примером применения метода тригонометрических сумм в теории чисел. Этот метод был развит далее в работах Г. Вейля и особенно И. М. Виноградова и представляет собой один из наиболее мощных методов аналитической теории чисел.
— Лежандра символ. Она явилась первым примером применения метода тригонометрических сумм в теории чисел. Этот метод был развит далее в работах Г. Вейля и особенно И. М. Виноградова и представляет собой один из наиболее мощных методов аналитической теории чисел.
4) Гаусса формулы для суммы гипергеометрического ряда. Если Re (c - b - a) > 0, то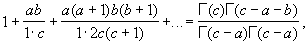
где Г (х) — гамма-функция. Опубликована в 1812.
С. Б. Стечкин.
| "БСЭ" >> "Г" >> "ГА" >> "ГАУ" |
Статья про "Гаусса формулы" в Большой Советской Энциклопедии была прочитана 580 раз
| Коптим скумбрию в коробке |
| Куриный суп |
TOP 20
- Лемке Михаил Константинович
- Сульфгидрильные группы
- «Казарменный коммунизм»
- Японское море
- Периодическая система элементов
- Глициния
- Башкирская Автономная Советская Социалистическая Республика
- Иммунитет (историч.)
- Андаманское море
- Сенсуализм
- Объединённая партия гаитянских коммунистов
- «Сообразительный»
- Балкано-кавказская раса
- Навигация (морск.)
- Звёздная астрономия
- Ямполь (пос. гор. типа в Донецкой обл.)
- Мандельштама - Бриллюэна рассеяние
- Кульчицкая Елена Львовна
- Театральные учебные заведения
- Электрическая постоянная