


БНБ
"БСЭ" (95279)
- Photogallery
- Естественные науки - Математика - Технология
- Авиация и машиностроение
- Высокие технологии
- Вычислительная техника
- Нанотехнология
- Роботехника
- Энергетика
- Электроника
Объём
Определение "Объём" в Большой Советской Энциклопедии
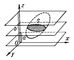 |
| Объём. Рис. |
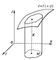 |
| Объём. Рис. |
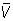 тела К. Если верхний объём
тела К. Если верхний объём 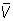 тела К совпадает с его нижним объёмом V, то число V =
тела К совпадает с его нижним объёмом V, то число V = 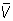 = V называется объёмом тела К, а само тело — кубируемым телом. Для того чтобы тело было кубируемым, необходимо и достаточно, чтобы для любого положительного числа e можно было указать такой описанный вокруг тела многогранник и такой вписанный в тело многогранник, разность Vd — Vi объёмов которых была бы меньше e.
= V называется объёмом тела К, а само тело — кубируемым телом. Для того чтобы тело было кубируемым, необходимо и достаточно, чтобы для любого положительного числа e можно было указать такой описанный вокруг тела многогранник и такой вписанный в тело многогранник, разность Vd — Vi объёмов которых была бы меньше e.
Аналитически Объём может быть выражен с помощью кратных интегралов. Пусть тело К (рис. 1) ограничено цилиндрической поверхностью с параллельными оси Oz образующими, квадрируемой областью М плоскости Оху и поверхностью z = f (x, у), которую любая параллель к образующей цилиндра пересекает в одной и только в одной точке. Объём такого тела может быть вычислен с помощью двойного интеграла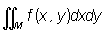 .
.
Объём тела, ограниченного замкнутой поверхностью, которая встречается с параллелью к оси Oz не более чем в двух точках, может быть вычислен как разность Объём двух тел, подобных предшествующему. Объём тела может быть выражен в виде тройного интеграла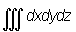 ,
,
где интегрирование распространяется на часть пространства, занятую телом. Иногда удобно вычислять Объём тел через его поперечные сечения. Пусть тело (рис.2), содержащееся между плоскостями z = а и z = b (b > а), рассекается плоскостями, перпендикулярными оси Oz. Если все сечения тела квадрируемы и площадь сечения S — непрерывная функция от z, то Объём тела может быть выражен простым интегралом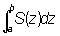 . (1)
. (1)
Исторически происходило так, что задолго до создания интегрального исчисления операция интегрирования фактически применялась (в различных геометрических формах) к вычислению Объём простейших тел (пирамиды, шара, некоторых тел вращения), чем и была подготовлена почва для оформления этого исчисления в 17—18 вв. В частности, формулу (1) содержал в зародыше т. н. Кавальери принцип, сохраняющий своё значение для школьного преподавания. В элементарном преподавании полезной оказывается также Симпсона формула, соответствующая тому случаю, когда в (1) функция S (z) является многочленом не выше 3-й степени.
Об обобщениях понятия «Объём» см. в ст. Мера множества.
Лит.: Кудрявцев Л. Д., Математический анализ, т. 1—2, М., 1970; Лебег А., Об измерении величин, пер. с франц., 2 изд., М., 1960.
| "БСЭ" >> "О" >> "ОБ" >> "ОБЪ" |
Статья про "Объём" в Большой Советской Энциклопедии была прочитана 954 раз
| Бургер двойного помола |
| Английская картошка фри |
TOP 20
- Лемке Михаил Константинович
- Сульфгидрильные группы
- «Казарменный коммунизм»
- Японское море
- Периодическая система элементов
- Глициния
- Башкирская Автономная Советская Социалистическая Республика
- Иммунитет (историч.)
- Андаманское море
- Сенсуализм
- Объединённая партия гаитянских коммунистов
- «Сообразительный»
- Балкано-кавказская раса
- Навигация (морск.)
- Звёздная астрономия
- Ямполь (пос. гор. типа в Донецкой обл.)
- Мандельштама - Бриллюэна рассеяние
- Кульчицкая Елена Львовна
- Театральные учебные заведения
- Электрическая постоянная