


БНБ
"БСЭ" (95279)
- Photogallery
- Естественные науки - Математика - Технология
- Авиация и машиностроение
- Высокие технологии
- Вычислительная техника
- Нанотехнология
- Роботехника
- Энергетика
- Электроника
Ортогональная система функций
Определение "Ортогональная система функций" в Большой Советской Энциклопедии
Ортогональная система функций, система функций {(jn (x)}, n = 1, 2,..., ортогональных с весом r (х) на отрезке [а, b], т. е. таких, что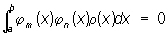
Примеры. Тригонометрическая система 1, cos nx, sin nx; n = 1, 2,..., - Ортогональная система функций с весом 1 на отрезке [-p, p]. Бесселя функции 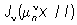 , где n = 1, 2,...,
, где n = 1, 2,..., 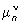 - положительные нули Jn(x), образуют для каждого n > - 1/2 Ортогональная система функций с весом х на отрезке [0, l ].
- положительные нули Jn(x), образуют для каждого n > - 1/2 Ортогональная система функций с весом х на отрезке [0, l ].
Если каждая функция j (х) из Ортогональная система функций такова, что 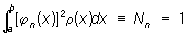 (условие нормированности), то такая система функций называется нормированной. Любую Ортогональная система функций можно нормировать, умножив j (х) на число
(условие нормированности), то такая система функций называется нормированной. Любую Ортогональная система функций можно нормировать, умножив j (х) на число 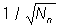 - нормирующий множитель.
- нормирующий множитель.
Систематическое изучение Ортогональная система функций было начато в связи с методом Фурье решения краевых задач уравнений математической физики. Этот метод приводит, например, к разысканию решений Штурма - Лиувилля задачи для уравнения [r(х) у" ]" + q (x) y = lу, удовлетворяющих граничным условиям у (а) + hy"(a) = 0, y (b) + Hy" (b) = 0, где h и Н - постоянные. Эти решения - т. н. собственные функции задачи - образуют Ортогональная система функций с весом r (х) на отрезке [a, b ].
Чрезвычайно важный класс Ортогональная система функций - ортогональные многочлены - был открыт П. Л. Чебышевым в его исследованиях по интерполированию способом наименьших квадратов и проблеме моментов. В 20 в. исследования по Ортогональная система функций проводятся в основном на базе теории интеграла и меры Лебега. Это способствовало выделению этих исследований в самостоятельный раздел математики. Одна из основных задач теории Ортогональная система функций- задача о разложении функции f (x) в ряд вида 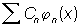 , где {jп (х)} - Ортогональная система функций Если положить формально
, где {jп (х)} - Ортогональная система функций Если положить формально 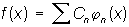 , где {jп (х)} - нормированная Ортогональная система функций, и допустить возможность почленного интегрирования, то, умножая этот ряд на jп (х) r(х) и интегрируя от а до b, получим:
, где {jп (х)} - нормированная Ортогональная система функций, и допустить возможность почленного интегрирования, то, умножая этот ряд на jп (х) r(х) и интегрируя от а до b, получим: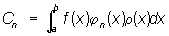 (*)
(*)
Коэффициенты Сп , называемые коэффициентами Фурье функции относительно системы {jn (x)}, обладают следующим экстремальным свойством: линейная форма 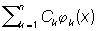 наилучшим образом приближает в среднем эту функцию. Иными словами, средняя квадратичная ошибка с весом r(х):
наилучшим образом приближает в среднем эту функцию. Иными словами, средняя квадратичная ошибка с весом r(х):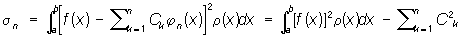 (*)
(*)
имеет наименьшее значение по сравнению с ошибками, даваемыми при том же n другими линейными выражениями вида 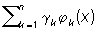 . Отсюда, в частности, получается т. н. неравенство Бесселя
. Отсюда, в частности, получается т. н. неравенство Бесселя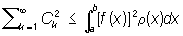
Ряд 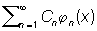 с коэффициентами Сп , вычисленными по формуле (*), называется рядом Фурье функции f (x) по нормированной Ортогональная система функций {jn (x)}. Для приложений первостепенную важность имеет вопрос, определяется ли однозначно функция f (x) своими коэффициентами Фурье. Ортогональная система функций, для которых это имеет место, называется полными, или замкнутыми. Условия замкнутости Ортогональная система функций могут быть даны в нескольких эквивалентных формах. 1) Любая непрерывная функция f (x) может быть с любой степенью точности приближена в среднем линейными комбинациями функций jk (x), то есть
с коэффициентами Сп , вычисленными по формуле (*), называется рядом Фурье функции f (x) по нормированной Ортогональная система функций {jn (x)}. Для приложений первостепенную важность имеет вопрос, определяется ли однозначно функция f (x) своими коэффициентами Фурье. Ортогональная система функций, для которых это имеет место, называется полными, или замкнутыми. Условия замкнутости Ортогональная система функций могут быть даны в нескольких эквивалентных формах. 1) Любая непрерывная функция f (x) может быть с любой степенью точности приближена в среднем линейными комбинациями функций jk (x), то есть 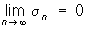 в этом случае говорят, что ряд
в этом случае говорят, что ряд 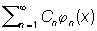 сходится в среднем к функции f (x)]. 2) Для всякой функции f (x), квадрат которой интегрируем относительно веса r(х), выполняется условие замкнутости Ляпунова - Стеклова:
сходится в среднем к функции f (x)]. 2) Для всякой функции f (x), квадрат которой интегрируем относительно веса r(х), выполняется условие замкнутости Ляпунова - Стеклова: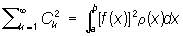
3) Не существует отличной от нуля функции с интегрируемым на отрезке [a, b ] квадратом, ортогональной ко всем функциям jn (x), n = 1, 2,....
Если рассматривать функции с интегрируемым квадратом как элементы гильбертова пространства, то нормированные Ортогональная система функций будут системами координатных ортов этого пространства, а разложение в ряд по нормированным Ортогональная система функций - разложением вектора по ортам. При этом подходе многие понятия теории нормированных Ортогональная система функций приобретают наглядный геометрический смысл. Например, формула (*) означает, что проекция вектора на орт равна скалярному произведению вектора и орта; равенство Ляпунова - Стеклова может быть истолковано как теорема Пифагора для бесконечномерного пространства: квадрат длины вектора равен сумме квадратов его проекций на оси координат; замкнутость Ортогональная система функций означает, что наименьшее замкнутое подпространство, содержащее все векторы этой системы, совпадает со всем пространством и т.д.
Лит.: Толстов Г. П., Ряды Фурье, 2 изд., М., 1960; Натансон И. П., Конструктивная теория функций, М. - Л., 1949; его же, Теория функций вещественной переменной, 2 изд., М., 1957; Джексон Д., Ряды Фурье и ортогональные полиномы, пер. с англ., М., 1948; Качмаж С., Штейнгауз Г., Теория ортогональных рядов, пер. с нем., М., 1958.
| "БСЭ" >> "О" >> "ОР" >> "ОРТ" |
Статья про "Ортогональная система функций" в Большой Советской Энциклопедии была прочитана 1490 раз
| Бургер двойного помола |
| Пицца в чугунной сковородке |
TOP 20
- Лемке Михаил Константинович
- Сульфгидрильные группы
- «Казарменный коммунизм»
- Японское море
- Периодическая система элементов
- Глициния
- Башкирская Автономная Советская Социалистическая Республика
- Иммунитет (историч.)
- Андаманское море
- Объединённая партия гаитянских коммунистов
- Сенсуализм
- «Сообразительный»
- Балкано-кавказская раса
- Навигация (морск.)
- Звёздная астрономия
- Ямполь (пос. гор. типа в Донецкой обл.)
- Мандельштама - Бриллюэна рассеяние
- Кульчицкая Елена Львовна
- Театральные учебные заведения
- Электрическая постоянная