


БНБ
"БСЭ" (95279)
- Photogallery
- Естественные науки - Математика - Технология
- Авиация и машиностроение
- Высокие технологии
- Вычислительная техника
- Нанотехнология
- Роботехника
- Энергетика
- Электроника
Пирсона кривые
Определение "Пирсона кривые" в Большой Советской Энциклопедии
Пирсона кривые, семейство кривых распределения [т. е. кривых у = у (х), изображающих зависимость плотности распределения от х], удовлетворяющих дифференциальному уравнению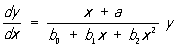 ,
,
где a, bo, b1, b2— действительные числа. Пирсона кривые классифицируются на 12 типов в зависимости от значения параметров а, b0, b1, b2 и интервала изменения х. Примерами Пирсона кривые являются нормальное распределение, Стьюдента распределение, распределение c2.
Всякая Пирсона кривые у (х) однозначно определяется заданием её первых четырёх моментов:
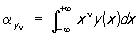 , n = 1, 2, 3, 4.
, n = 1, 2, 3, 4.
На основании этого свойства Пирсона кривые иногда используются в математической статистике для приближённого представления неизвестной плотности р (х). Пусть, например, имеется большой ряд независимых наблюдений x1, x2,..., xn случайной величины Х с неизвестной плотностью распределения р (х). Применяя метод моментов (см. Статистические оценки), полагают 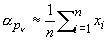 и для приближённого представления р (х) выбирают такую Пирсона кривые y (x), для которой
и для приближённого представления р (х) выбирают такую Пирсона кривые y (x), для которой 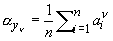 , где n = 1, 2, 3, 4.
, где n = 1, 2, 3, 4.
Пирсона кривые впервые были применены для построения эмпирических плотностей английским математиком К. Пирсоном в 1894.
Лит.: Кендалл М., Стьюарт А., Теория распределений, пер. с англ., М., 1966.
| "БСЭ" >> "П" >> "ПИ" >> "ПИР" >> "ПИРС" |
Статья про "Пирсона кривые" в Большой Советской Энциклопедии была прочитана 605 раз
| Бургер двойного помола |
| Луковый соус |
TOP 20
- Лемке Михаил Константинович
- Сульфгидрильные группы
- «Казарменный коммунизм»
- Японское море
- Периодическая система элементов
- Глициния
- Башкирская Автономная Советская Социалистическая Республика
- Иммунитет (историч.)
- Андаманское море
- Объединённая партия гаитянских коммунистов
- Сенсуализм
- «Сообразительный»
- Балкано-кавказская раса
- Навигация (морск.)
- Звёздная астрономия
- Ямполь (пос. гор. типа в Донецкой обл.)
- Мандельштама - Бриллюэна рассеяние
- Кульчицкая Елена Львовна
- Театральные учебные заведения
- Электрическая постоянная