Симметрия (в математике)

Определение "Симметрия (в математике)" в Большой Советской Энциклопедии

Винтовая симметрия

Симметрия (от греч. symmetria - соразмерность) в математике,
1) симметрия (в узком смысле), или отражение (зеркальное) относительно плоскости a в пространстве (относительно прямой а на плоскости), - преобразование пространства (плоскости), при котором каждая точка М переходит в точку M" такую, что отрезок MM" перпендикулярен плоскости a (прямой а) и делится ею пополам. Плоскость a (прямая а) называется плоскостью (осью) Симметрия (в математике)

Зеркально-осевая симметрия. Многогранник

Отражение - пример ортогонального преобразования, изменяющего ориентацию (в отличие от собственного движения). Любое ортогональное преобразование можно осуществить последовательным выполнением конечного числа отражений - этот факт играет существенную роль в исследовании Симметрия (в математике) геометрических фигур.

Плоская симметричная фигура

2) Симметрия (в широком смысле) - свойство геометрической фигуры Ф, характеризующее некоторую правильность формы Ф, неизменность её при действии движений и отражений. Точнее, фигура Ф обладает Симметрия (в математике) (симметрична), если существует нетождественное ортогональное преобразование, переводящее эту фигуру в себя. Совокупность всех ортогональных преобразований, совмещающих фигуру Ф с самой собой, является группой, называемой группой симметрии этой фигуры (иногда сами эти преобразования называются симметриями).

Симметрия. Бордюр

Так, плоская фигура, преобразующаяся в себя при отражении, симметрична относительно прямой - оси Симметрия (в математике) (рис. 1); здесь группа симметрии состоит из двух элементов. Если фигура Ф на плоскости такова, что повороты относительно какой-либо точки О на угол 360°/n, n - целое число ³ 2, переводят её в себя, то Ф обладает Симметрия (в математике) n-го порядка относительно точки О - центра Симметрия (в математике) Примером таких фигур являются правильные многоугольники (рис. 2); группа Симметрия (в математике) здесь - т. н. циклическая группа n-го порядка. Окружность обладает Симметрия (в математике) бесконечного порядка (поскольку совмещается с собой поворотом на любой угол).

Симметрия восьмого порядка. Правильный многоугольник

Простейшими видами пространственной Симметрия (в математике), помимо Симметрия (в математике), порожденной отражениями, являются центральная Симметрия (в математике), осевая Симметрия (в математике) и Симметрия (в математике) переноса.

Симметрия. Орнамент

а) В случае центральной симметрии (инверсии) относительно точки О фигура Ф совмещается сама с собой после последовательных отражений от трёх взаимно перпендикулярных плоскостей, другими словами, точка О - середина отрезка, соединяющего симметричные точки Ф (рис. 3). б) В случае осевой симметрии, или Симметрия (в математике) относительно прямой n-го порядка, фигура накладывается на себя вращением вокруг некоторой прямой (оси Симметрия (в математике)) на угол 360°/n. Например, куб имеет прямую AB осью Симметрия (в математике) третьего порядка, а прямую CD - осью Симметрия (в математике) четвёртого порядка (рис. 3); вообще, правильные и полуправильные многогранники симметричны относительно ряда прямых. Расположение, количество и порядок осей Симметрия (в математике) играют важную роль в кристаллографии (см. Симметрия кристаллов), в) Фигура, накладывающаяся на себя последовательным вращением на угол 360°/2k вокруг прямой AB и отражением в плоскости, перпендикулярной к ней, имеет зеркально-осевую Симметрия (в математике) Прямая AB, называется зеркально-поворотной осью Симметрия (в математике) порядка 2k, является осью Симметрия (в математике) порядка k (рис. 4). Зеркально-осевая Симметрия (в математике) порядка 2 равносильна центральной Симметрия (в математике) г) В случае симметрии переноса фигура накладывается на себя переносом вдоль некоторой прямой (оси переноса) на какой-либо отрезок. Например, фигура с единственной осью переноса обладает бесконечным множеством плоскостей Симметрия (в математике) (поскольку любой перенос можно осуществить двумя последовательными отражениями от плоскостей, перпендикулярных оси переноса) (рис. 5). Фигуры, имеющие несколько осей переноса, играют важную роль при исследовании кристаллических решёток.

Симметрия переноса

В искусстве Симметрия (в математике) получила распространение как один из видов гармоничной композиции. Она свойственна произведениям архитектуры (являясь непременным качеством если не всего сооружения в целом, то его частей и деталей - плана, фасада, колонн, капителей и т. д.) и декоративно-прикладного искусства. Симметрия (в математике) используется также в качестве основного приёма построения бордюров и орнаментов (плоских фигур, обладающих соответственно одной или несколькими Симметрия (в математике) переноса в сочетании с отражениями) (рис. 6, 7).

Симметрия третьего порядка. Куб

Комбинации Симметрия (в математике), порожденные отражениями и вращениями (исчерпывающие все виды Симметрия (в математике) геометрических фигур), а также переносами, представляют интерес и являются предметом исследования в различных областях естествознания. Например, винтовая Симметрия (в математике), осуществляемая поворотом на некоторый угол вокруг оси, дополненным переносом вдоль той же оси, наблюдается в расположении листьев у растений (рис. 8) (подробнее см. в ст. Симметрия в биологии). Симметрия (в математике) конфигурации молекул, сказывающаяся на их физических и химических характеристиках, имеет значение при теоретическом анализе строения соединений, их свойств и поведения в различных реакциях (см. Симметрия в химии). Наконец, в физических науках вообще, помимо уже указанной геометрической Симметрия (в математике) кристаллов и решёток, приобретают важное значение представления о Симметрия (в математике) в общем смысле (см. ниже). Так, симметричность физического пространства-времени, выражающаяся в его однородности и изотропности (см. Относительности теория), позволяет установить т. н. сохранения законы; обобщённая Симметрия (в математике) играет существенную роль в образовании атомных спектров и в классификации элементарных частиц (см. Симметрия в физике).

3) Симметрия (в общем смысле) означает инвариантность структуры математического (или физического) объекта относительно его преобразований. Например, Симметрия (в математике) законов теории относительности определяется инвариантностью их относительно Лоренца преобразований. Определение совокупности преобразований, оставляющих без изменения все структурные соотношения объекта, т. е. определение группы G его автоморфизмов, стало руководящим принципом современной математики и физики, позволяющим глубоко проникнуть во внутреннее строение объекта в целом и его частей.

Поскольку такой объект можно представить элементами некоторого пространства Р, наделённого соответствующей характерной для него структурой, постольку преобразования объекта являются преобразованиями Р. Т. о. получается представление группы G в группе преобразований Р (или просто в Р), а исследование Симметрия (в математике) объекта сводится к исследованию действия G на Р и отысканию инвариантов этого действия. Точно так же Симметрия (в математике) физических законов, управляющих исследуемым объектом и обычно описывающихся уравнениями, которым удовлетворяют элементы пространства Р, определяется действием G на такие уравнения.

Так, например, если некоторое уравнение линейно на линейном же пространстве Р и остаётся инвариантным при преобразованиях некоторой группы G, то каждому элементу g из G соответствует линейное преобразование T_g в линейном пространстве R решений этого уравнения. Соответствие g ® T_g является линейным представлением G и знание всех таких её представлений позволяет устанавливать различные свойства решений, а также помогает находить во многих случаях (из «соображений симметрии») и сами решения. Этим, в частности, объясняется необходимость для математики и физики развитой теории линейных представлений групп. Конкретные примеры см. в ст. Симметрия в физике.

Лит.: Шубников А. В., Симметрия. (Законы симметрии и их применение в науке, технике и прикладном искусстве), М. - Л., 1940; Кокстер Г. Симметрия (в математике) М., Введение в геометрию, пер. с англ., М., 1966; Вейль Г., Симметрия, пер. с англ., М., 1968; Вигнер Е., Этюды о симметрии, пер. с англ., М., 1971.
  М. И. Войцеховский.

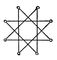
Рис. 2. Звездчатый правильный многоугольник, обладающий симметрией восьмого порядка относительно своего центра.


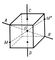
Рис. 3. Куб, имеющий прямую AB осью симметрии третьего порядка, прямую CD - осью симметрии четвёртого порядка, точку О - центром симметрии. Точки М и M" куба симметричны как относительно осей AB и CD, так и относительно центра О.