


БНБ
"БСЭ" (95279)
- Photogallery
- Естественные науки - Математика - Технология
- Авиация и машиностроение
- Высокие технологии
- Вычислительная техника
- Нанотехнология
- Роботехника
- Энергетика
- Электроника
Симметрия (в физике)
Определение "Симметрия (в физике)" в Большой Советской Энциклопедии
Симметрия в физике. Если законы, устанавливающие соотношения между величинами, характеризующими физическую систему, или определяющие изменение этих величин со временем, не меняются при определённых операциях (преобразованиях), которым может быть подвергнута система, то говорят, что эти законы обладают Симметрия (в физике) (или инвариантны) относительно данных преобразований. В математическом отношении преобразования Симметрия (в физике) составляют группу.
Опыт показывает, что физические законы симметричны относительно следующих наиболее общих преобразований.
Непрерывные преобразования
1) Перенос (сдвиг) системы как целого в пространстве. Это и последующие пространственно-временные преобразования можно понимать в двух смыслах: как активное преобразование — реальный перенос физической системы относительно выбранной системы отсчёта или как пассивное преобразование — параллельный перенос системы отсчёта. Симметрия (в физике) физических законов относительно сдвигов в пространстве означает эквивалентность всех точек пространства, т. е. отсутствие в пространстве каких-либо выделенных точек (однородность пространства).
2) Поворот системы как целого в пространстве. Симметрия (в физике) физических законов относительно этого преобразования означает эквивалентность всех направлений в пространстве (изотропию пространства).
3) Изменение начала отсчёта времени (сдвиг во времени). Симметрия (в физике) относительно этого преобразования означает, что физические законы не меняются со временем.
4) Переход к системе отсчёта, движущейся относительно данной системы с постоянной (по направлению и величине) скоростью. Симметрия (в физике) относительно этого преобразования означает, в частности, эквивалентность всех инерциальных систем отсчёта (см. Относительности теория).
5) Калибровочные преобразования. Законы, описывающие взаимодействия частиц, обладающих каким-либо зарядом (электрическим зарядом, барионным зарядом, лептонным зарядом, гиперзарядом), симметричны относительно калибровочных преобразований 1-го рода. Эти преобразования заключаются в том, что волновые функции всех частиц могут быть одновременно умножены на произвольный фазовый множитель: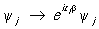 ,
, 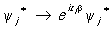 , (1)
, (1)
где yj — волновая функция частицы j, 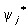 — комплексно сопряжённая ей функция, zj — соответствующий частице заряд, выраженный в единицах элементарного заряда (например, элементарного электрического заряда е), b — произвольный числовой множитель.
— комплексно сопряжённая ей функция, zj — соответствующий частице заряд, выраженный в единицах элементарного заряда (например, элементарного электрического заряда е), b — произвольный числовой множитель.
Наряду с этим электромагнитные взаимодействия симметричны относительно калибровочных (градиентных) преобразований 2-го рода для потенциалов электромагнитного поля (А, j):
А ® А + grad f, 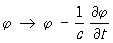 , (2)
, (2)
где f (x, у, z, t) — произвольная функция координат (х, у, z) и времени (t), с — скорость света. Чтобы преобразования (1) и (2) в случае электромагнитных полей выполнялись одновременно, следует обобщить калибровочные преобразования 1-го рода: необходимо потребовать, чтобы законы взаимодействия были симметричны относительно преобразований (1) с величиной b, являющейся произвольной функцией координат и времени: 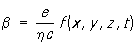 , где
, где 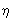 — Планка постоянная. Связь калибровочных преобразований 1-го и 2-го рода для электромагнитных взаимодействий обусловлена двоякой ролью электрического заряда: с одной стороны, электрический заряд является сохраняющейся величиной, а с другой — он выступает как константа взаимодействия, характеризующая связь электромагнитного поля с заряженными частицами.
— Планка постоянная. Связь калибровочных преобразований 1-го и 2-го рода для электромагнитных взаимодействий обусловлена двоякой ролью электрического заряда: с одной стороны, электрический заряд является сохраняющейся величиной, а с другой — он выступает как константа взаимодействия, характеризующая связь электромагнитного поля с заряженными частицами.
Преобразования (1) отвечают законам сохранения различных зарядов (см. ниже), а также некоторым внутренним Симметрия (в физике) взаимодействия. Если заряды являются не только сохраняющимися величинами, но и источниками полей (как электрический заряд), то соответствующие им поля должны быть также калибровочными полями (аналогично электромагнитным полям), а преобразования (1) обобщаются на случай, когда величины b являются произвольными функциями координат и времени (и даже операторами, преобразующими состояния внутренней Симметрия (в физике)). Такой подход в теории взаимодействующих полей приводит к различным калибровочным теориям сильных и слабых взаимодействий (т. н. Янга — Милса теория).
6) Изотопическая инвариантность сильных взаимодействий. Сильные взаимодействия симметричны относительно поворотов в особом «изотоническом пространстве». Одним из проявлений этой Симметрия (в физике) является зарядовая независимость ядерных сил, заключающаяся в равенстве сильных взаимодействий нейтронов с нейтронами, протонов с протонами и нейтронов с протонами (если они находятся соответственно в одинаковых состояниях). Изотопическая инвариантность является приближённой Симметрия (в физике), нарушаемой электромагнитными взаимодействиями. Она представляет собой часть более широкой приближённой Симметрия (в физике) сильных взаимодействий — SU (3)-C. (см. Сильные взаимодействия).
Дискретные преобразования
Перечисленные выше типы Симметрия (в физике) характеризуются параметрами, которые могут непрерывно изменяться в некоторой области значений (например, сдвиг в пространстве характеризуется тремя параметрами смещения вдоль каждой из координатных осей, поворот — тремя углами вращения вокруг этих осей и т. д.). Наряду с непрерывными Симметрия (в физике) большое значение в физике имеют дискретные Симметрия (в физике) Основные из них следующие.
1) Пространственная инверсия (Р). Относительно этого преобразования симметричны процессы, вызванные сильным и электромагнитным взаимодействиями. Указанные процессы одинаково описываются в двух различных декартовых системах координат, получаемых одна из другой изменением направлений осей координат на противоположные (т. н. переход от «правой» к «левой» системе координат). Это преобразование может быть получено также зеркальным отражением относительно трёх взаимно перпендикулярных плоскостей; поэтому Симметрия (в физике) по отношению к пространственной инверсии называемой обычно зеркальной Симметрия (в физике) Наличие зеркальной Симметрия (в физике) означает, что если в природе осуществляется какой-либо процесс, обусловленный сильным или электромагнитным взаимодействием, то может осуществиться и другой процесс, протекающий с той же вероятностью и являющийся как бы «зеркальным изображением» первого. При этом физические величины, характеризующие оба процесса, будут связаны определённым образом. Например, скорости частиц и напряжённости электрического поля изменят направления на противоположные, а направления напряжённости магнитного поля и момента количества движения не изменятся.
Нарушением такой Симметрия (в физике) представляются явления (например, правое или левое вращение плоскости поляризации света), происходящие в веществах-изомерах (оптическая изомерия). В действительности, однако, зеркальная Симметрия (в физике) в таких явлениях не нарушена: она проявляется в том, что для любого, например левовращающего, вещества существует аналогичное по химическому составу вещество, молекулы которого являются «зеркальным изображением» молекул первого и которое будет правовращающим.
Нарушение зеркальной Симметрия (в физике) наблюдается в процессах, вызванных слабым взаимодействием.
2) Преобразование замены всех частиц на античастицы (зарядовое сопряжение, С). Симметрия (в физике) относительно этого преобразования также имеет место для процессов, происходящих в результате сильного и электромагнитного взаимодействий, и нарушается в процессах слабого взаимодействия. При преобразовании зарядового сопряжения меняются на противоположные значения заряды частиц, напряжённости электрического и магнитного полей.
3) Последовательное проведение (произведение) преобразований инверсии и зарядового сопряжения (комбинированная инверсия, СР). Поскольку сильные и электромагнитные взаимодействия симметричны относительно каждого из этих преобразований, они симметричны и относительно комбинированной инверсии. Однако относительно этого преобразования оказываются симметричными и слабые взаимодействия, которые не обладают Симметрия (в физике) по отношению к преобразованию инверсии и зарядовому сопряжению в отдельности. Симметрия (в физике) процессов слабого взаимодействия относительно комбинированной инверсии может быть указанием на то, что отсутствие зеркальной Симметрия (в физике) в них связано со структурой элементарных частиц и что античастицы по своей структуре являются как бы «зеркальным изображением» соответствующих частиц. В этом смысле процессы слабого взаимодействия, происходящие с какими-либо частицами, и соответствующие процессы с их античастицами связаны между собой так же, как явления в оптических изомерах.
Открытие распадов долгоживущих K0L-мезонов на 2 p-мезона и наличие зарядовой асимметрии в распадах K0L ® p+ + e- + ne (p+ + m- + nm) и K0L ® p- + е+ + nе (p-+ m+ + nm) (см. К-мезоны) указывают на существование сил, несимметричных относительно комбинированной инверсии. Пока не установлено, являются ли эти силы малыми добавками к известным фундаментальным взаимодействиям (сильному, электромагнитному, слабому) или же имеют особую природу. Нельзя также исключить возможность того, что нарушение СР-Симметрия (в физике) связано с особыми геометрическими свойствами пространства-времени на малых интервалах.
4) Преобразование изменения знака времени (обращение времени, Т). По отношению к этому преобразованию симметричны все элементарные процессы, протекающие в результате сильного, электромагнитного и слабого взаимодействий (за исключением распадов K0L-meзонов).
5) Произведение трёх преобразований: зарядового сопряжения С, инверсии Р и обращения времени Т (СРТ-симметрия; см. СРТ-теорема). СРТ-Симметрия (в физике) вытекает из общих принципов квантовой теории поля. Она связана главным образом с Симметрия (в физике) относительно Лоренца преобразований и локальностью взаимодействия (т. е. с взаимодействием полей в одной точке). Эта Симметрия (в физике) должна была бы выполняться, даже если бы взаимодействия были несимметричны относительно каждого из преобразований С, Р и Т в отдельности. Следствием СРТ-инвариантности является т. н. перекрёстная (кроссинг) Симметрия (в физике) в описании процессов, происходящих с частицами и античастицами. Так, например, три реакции — упругое рассеяние какой-либо частицы a на частице b: a + b ® a + b, упругое рассеяние античастицы 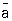 на частице b:
на частице b: 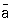 + b ®
+ b ® 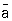 + b и аннигиляция частицы а и её античастицы
+ b и аннигиляция частицы а и её античастицы 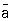 в пару частиц b,
в пару частиц b, 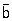 : а +
: а + 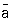 ® b +
® b + 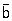 описываются единой аналитической функцией (зависящей от квадрата полной энергии системы и квадрата переданного импульса), которая в различных областях изменения этих переменных даёт амплитуду каждого из указанных процессов.
описываются единой аналитической функцией (зависящей от квадрата полной энергии системы и квадрата переданного импульса), которая в различных областях изменения этих переменных даёт амплитуду каждого из указанных процессов.
6) Преобразование перестановки одинаковых частиц. Волновая функция системы, содержащей одинаковые частицы, симметрична относительно перестановки любой пары одинаковых частиц (т. е. их координат и спинов) с целым, в частности нулевым, спином и антисимметрична относительно такой перестановки для частиц с полуцелым спином (см. Квантовая механика).
Симметрия и законы сохранения
Согласно Нётер теореме, каждому преобразованию Симметрия (в физике), характеризуемому одним непрерывно изменяющимся параметром, соответствует величина, которая сохраняется (не меняется со временем) для системы, обладающей этой Симметрия (в физике) Из Симметрия (в физике) физических законов относительно сдвига замкнутой системы в пространстве, поворота её как целого и изменения начала отсчёта времени следуют соответственно законы сохранения импульса, момента количества движения и энергии. Из Симметрия (в физике) относительно калибровочных преобразований 1-го рода — законы сохранения зарядов (электрического, барионного и др.), из изотопической инвариантности — сохранение изотопического спина в процессах сильного взаимодействия. Что касается дискретных Симметрия (в физике), то в классической механике они не приводят к каким-либо законам сохранения. Однако в квантовой механике, в которой состояние системы описывается волновой функцией, или для волновых полей (например, электромагнитного поля), где справедлив суперпозиции принцип, из существования дискретных Симметрия (в физике) следуют законы сохранения некоторых специфических величин, не имеющих аналогов в классической механике. Существование таких величин можно продемонстрировать на примере пространственной чётности, сохранение которой вытекает из Симметрия (в физике) относительно пространственной инверсии. Действительно, пусть y1 — волновая функция, описывающая какое-либо состояние системы, а y2 — волновая функция системы, получающаяся в результате пространств. инверсии (символически: y2 = Рy1, где Р — оператор пространств. инверсии). Тогда, если существует Симметрия (в физике) относительно пространственной инверсии, y2 является одним из возможных состояний системы и, согласно принципу суперпозиции, возможными состояниями системы являются суперпозиции y1 и y2: симметричная комбинация ys = y1 + y2 и антисимметричная yа = y1 — y2. При преобразованиях инверсии состояние y2 не меняется (т. к. Pys = Py1 + Py2 = y2 + y1 = ys), а состояние ya меняет знак (Pya = Py1 — Py2 = y2 — y1 = — ya). В первом случае говорят, что пространственная чётность системы положительна (+1), во втором — отрицательна (—1). Если волновая функция системы задаётся с помощью величин, которые не меняются при пространственной инверсии (таких, например, как момент количества движения и энергия), то вполне определённое значение будет иметь и чётность системы. Система будет находиться в состоянии либо с положительной, либо с отрицательной чётностью (причём переходы из одного состояния в другое под действием сил, симметричных относительно пространственной инверсии, абсолютно запрещены).
Аналогично, из Симметрия (в физике) относительно зарядового сопряжения и комбинированной инверсии следует существование зарядовой чётности (С-чётности) и комбинированной чётности (СР-чётности). Эти величины, однако, могут служить характеристикой только для абсолютно нейтральных (обладающих нулевыми значениями всех зарядов) частиц или систем. Действительно, система с отличным от нуля зарядом при зарядовом сопряжении переходит в систему с противоположным знаком заряда, и поэтому невозможно составить суперпозицию этих двух состояний, не нарушая закона сохранения заряда. Вместе с тем для характеристики системы сильно взаимодействующих частиц (адронов) с нулевыми барионным зарядом и странностью (или гиперзарядом), но отличным от нуля электрическим зарядом, можно ввести т. н. G-чётность. Эта характеристика возникает из изотопической инвариантности сильных взаимодействий (которую можно трактовать как Симметрия (в физике) относительно преобразования поворота в «изотопическом пространстве») и зарядового сопряжения. Примером такой системы может служить пи-мезон. См. также ст. Сохранения законы.
Симметрия квантово-механических систем и стационарные состояния. Вырождение
Сохранение величин, отвечающих различным Симметрия (в физике) квантово-механические системы, является следствием того, что соответствующие им операторы коммутируют с гамильтонианом системы, если он не зависит явно от времени (см. Квантовая механика, Перестановочные соотношения). Это означает, что указанные величины измеримы одновременно с энергией системы, т. е. могут принимать вполне определённые значения при заданном значении энергии. Поэтому из них можно составить т. н. полный набор величин, определяющих состояние системы. Т. о., стационарные состояния (состояния с заданной энергией) системы определяются величинами, отвечающими Симметрия (в физике) рассматриваемой системы.
Наличие Симметрия (в физике) приводит к тому, что различные состояния движения квантовомеханической системы, которые получаются друг из друга преобразованием Симметрия (в физике), обладают одинаковыми значениями физических величин, не меняющихся при этих преобразованиях. Т. о., Симметрия (в физике) системы, как правило, ведёт к вырождению. Например, определённому значению энергии системы может отвечать несколько различных состояний, преобразующихся друг через друга при преобразованиях Симметрия (в физике) В математическом отношении эти состояния представляют базис неприводимого представления группы Симметрия (в физике) системы (см. Группа). Это обусловливает плодотворность применения методов теории групп в квантовой механике.
Помимо вырождения уровней энергии, связанного с явной Симметрия (в физике) системы (например, относительно поворотов системы как целого), в ряде задач существует дополнительное вырождение, связанное с т. н. скрытой Симметрия (в физике) взаимодействия. Такие скрытые Симметрия (в физике) существуют, например, для кулоновского взаимодействия и для изотропного осциллятора.
Если система, обладающая какой-либо Симметрия (в физике), находится в поле сил, нарушающих эту Симметрия (в физике) (но достаточно слабых, чтобы их можно было рассматривать как малое возмущение), происходит расщепление вырожденных уровней энергии исходной системы: различные состояния, которые в силу Симметрия (в физике) системы имели одинаковую энергию, под действием «несимметричного» возмущения приобретают различные энергетические смещения. В случаях, когда возмущающее поле обладает некоторой Симметрия (в физике), составляющей часть Симметрия (в физике) исходной системы, вырождение уровней энергии снимается не полностью: часть уровней остаётся вырожденной в соответствии с Симметрия (в физике) взаимодействия, «включающего» возмущающее поле.
Наличие в системе вырожденных по энергии состояний, в свою очередь, указывает на существование Симметрия (в физике) взаимодействия и позволяет в принципе найти эту Симметрия (в физике), когда она заранее не известна. Последнее обстоятельство играет важнейшую роль, например, в физике элементарных частиц. Существование групп частиц с близкими массами и одинаковыми др. характеристиками, но различными электрическими зарядами (т. н. изотопических мультиплетов) позволило установить изотопическую инвариантность сильных взаимодействий, а возможность объединения частиц с одинаковыми свойствами в более широкие группы привело к открытию SU (3)-C. сильного взаимодействия и взаимодействий, нарушающих эту Симметрия (в физике) (см. Сильные взаимодействия). Существуют указания, что сильное взаимодействие обладает ещё более широкой группой Симметрия (в физике)
Весьма плодотворно понятие т. н. динамической Симметрия (в физике) системы, которое возникает, когда рассматриваются преобразования, включающие переходы между состояниями системы с различными энергиями. Неприводимым представлением группы динамической Симметрия (в физике) будет весь спектр стационарных состояний системы. Понятие динамической Симметрия (в физике) можно распространить и на случаи, когда гамильтониан системы зависит явно от времени, причём в одно неприводимое представление динамической группы Симметрия (в физике) объединяются в этом случае все состояния квантово-механической системы, не являющиеся стационарными (т. е. не обладающие заданной энергией).
Лит.: Вигнер Е., Этюды о симметрии, пер. с англ., М., 1971.
Симметрия (в физике) Симметрия (в физике) Герштейн.
| "БСЭ" >> "С" >> "СИ" >> "СИМ" >> "СИММ" |
Статья про "Симметрия (в физике)" в Большой Советской Энциклопедии была прочитана 1503 раз
| Английский рыбный пирог |
| Английский рыбный пирог |
TOP 20
- Лемке Михаил Константинович
- Сульфгидрильные группы
- «Казарменный коммунизм»
- Японское море
- Периодическая система элементов
- Глициния
- Башкирская Автономная Советская Социалистическая Республика
- Объединённая партия гаитянских коммунистов
- Иммунитет (историч.)
- Андаманское море
- Сенсуализм
- «Сообразительный»
- Балкано-кавказская раса
- Навигация (морск.)
- Звёздная астрономия
- Ямполь (пос. гор. типа в Донецкой обл.)
- Мандельштама - Бриллюэна рассеяние
- Кульчицкая Елена Львовна
- Театральные учебные заведения
- Электрическая постоянная