


БНБ
"БСЭ" (95279)
- Photogallery
- Естественные науки - Математика - Технология
- Авиация и машиностроение
- Высокие технологии
- Вычислительная техника
- Нанотехнология
- Роботехника
- Энергетика
- Электроника
«Хи-квадрат» распределение
Определение "«Хи-квадрат» распределение" в Большой Советской Энциклопедии
«Хи-квадрат» распределение с f степенями свободы, распределение вероятностей суммы квадратов
c2 = X12+...+Xf2,
независимых случайных величин X1,..., Xf, подчиняющихся нормальному распределению с нулевым математическим ожиданием и единичной дисперсией. Функция «Х.-к.» р. выражается интегралом ,
, 
Первые три момента (математическое ожидание дисперсия и третий центральный момент) суммы c2 равны соответственно f, 2f, 8f. Сумма двух независимых случайных величин c12 и c22, с f1 и f2 степенями свободы подчиняется «Х.-к.» р. с f1 + f2 степенями свободы.
Примерами «Х.-к.» р. могут служить распределения квадратов случайных величин, подчиняющихся Рэлея распределению и Максвелла распределению. В терминах «Х.-к.» р. с чётным числом степеней свободы выражается Пуассона распределение: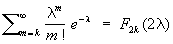 .
.
Если количество слагаемых f суммы c2 неограниченно увеличивается, то согласно центральной предельной теореме распределение нормированного отношения  сходится к стандартному нормальному распределению:
сходится к стандартному нормальному распределению: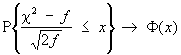 ,
,
где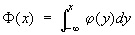
 .
.
Следствием этого факта является другое предельное соотношение, удобное для вычисления Ff (x) при больших значениях f:
В математической статистике «Х.-к.» р. используется для построения интервальных оценок и статистических критериев. Если Y1,..., Yn — случайные величины, представляющие собой результаты независимых измерений неизвестной постоянной а, причём ошибки измерений Yi — а независимы, распределены одинаково нормально и
Е (Yi — a) = 0, Е (Yi — а)2 = s2,
то статистическая оценка неизвестной дисперсии s2 выражается формулой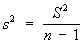 ,
,
где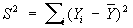 ,
, 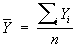 .
.
Отношение S2/s2 подчиняется «Х.-к.» р. с f = n — 1 степенями свободы. Пусть x1 и x2 — положительные числа, являющиеся решениями уравнений Ff (x1) = a/2 и Ff (x2) = 1 — a/2 [a — заданное число из интервала (0, 1/2)]. В таком случае
Р {х1 < S2/s2 < x2) = Р {S2/x2 < s2 < S2/x1} = 1—a.
Интервал (S2/x1, S2/x2) называют доверительным интервалом для s2, соответствующим коэффициенту доверия 1 — a. Такой способ построения интервальной оценки для s2 часто применяется с целью проверки гипотезы, согласно которой s2 = s02(s02 — заданное число): если s02 принадлежит указанному доверительному интервалу, то делается заключение, что результаты измерений не противоречат гипотезе s2 = s02. Если же
то нужно считать, что s2 > s02 или s2 < s02 соответственно. Такому критерию отвечает значимости уровень, равный a.
Лит.: Крамер Г., Математические методы статистики, пер. с англ., 2 изд., М., 1975.
Л. Н. Большев.
| "БСЭ" >> "Х" >> "ХИ" >> "ХИК" |
Статья про "«Хи-квадрат» распределение" в Большой Советской Энциклопедии была прочитана 847 раз
| Коптим скумбрию в коробке |
| Английское куриное карри |
TOP 20
- Лемке Михаил Константинович
- Сульфгидрильные группы
- «Казарменный коммунизм»
- Японское море
- Периодическая система элементов
- Объединённая партия гаитянских коммунистов
- Глициния
- Башкирская Автономная Советская Социалистическая Республика
- Иммунитет (историч.)
- Андаманское море
- Сенсуализм
- Балкано-кавказская раса
- «Сообразительный»
- Навигация (морск.)
- Звёздная астрономия
- Ямполь (пос. гор. типа в Донецкой обл.)
- Мандельштама - Бриллюэна рассеяние
- Кульчицкая Елена Львовна
- Театральные учебные заведения
- Электрическая постоянная