


БНБ
"БСЭ" (95279)
- Photogallery
- Естественные науки - Математика - Технология
- Авиация и машиностроение
- Высокие технологии
- Вычислительная техника
- Нанотехнология
- Роботехника
- Энергетика
- Электроника
Линейный оператор
Определение "Линейный оператор" в Большой Советской Энциклопедии
Линейный оператор, обобщение понятия линейного преобразования на линейные пространства. Линейным оператором F на линейном пространстве Е называют функцию F(x), определённую для всех х Î Е, значения которой суть элементы линейного пространства E1, и обладающую свойством линейности:
где х и у — любые элементы из Е, a и b — числа. Если пространства Е и E1 нормированы и величина  ограничена, то Линейный оператор F называют ограниченным, а
ограничена, то Линейный оператор F называют ограниченным, а 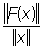 его нормой.
его нормой.
Важнейшими конкретными примерами Линейный оператор в функциональных пространствах являются дифференциальные Линейный оператор
и интегральные Линейный оператор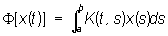
примером Линейный оператор функций многих переменных может служить Лапласа оператор. Теория Линейный оператор находит большое применение в различных вопросах математической физики и прикладной математики. См. также Функциональный анализ, Операторов теория, Спектральный анализ (математический), Собственные значения и собственные функции, Собственные векторы.
| "БСЭ" >> "Л" >> "ЛИ" >> "ЛИН" >> "ЛИНЕ" |
Статья про "Линейный оператор" в Большой Советской Энциклопедии была прочитана 764 раз
| Коптим скумбрию в коробке |
| Луковый соус |
TOP 20
- Лемке Михаил Константинович
- Сульфгидрильные группы
- «Казарменный коммунизм»
- Японское море
- Периодическая система элементов
- Глициния
- Башкирская Автономная Советская Социалистическая Республика
- Иммунитет (историч.)
- Объединённая партия гаитянских коммунистов
- Андаманское море
- Сенсуализм
- «Сообразительный»
- Балкано-кавказская раса
- Навигация (морск.)
- Звёздная астрономия
- Ямполь (пос. гор. типа в Донецкой обл.)
- Мандельштама - Бриллюэна рассеяние
- Кульчицкая Елена Львовна
- Театральные учебные заведения
- Электрическая постоянная