


БНБ
"БСЭ" (95279)
- Photogallery
- Естественные науки - Математика - Технология
- Авиация и машиностроение
- Высокие технологии
- Вычислительная техника
- Нанотехнология
- Роботехника
- Энергетика
- Электроника
Связи механические
Определение "Связи механические" в Большой Советской Энциклопедии
Связи механические, ограничения, налагаемые на положение или движение механической системы. Обычно Связи механические осуществляются с помощью каких-нибудь тел. Примеры таких Связи механические: поверхность, по которой скользит или катится тело; нить, на которой подвешен груз; шарниры, соединяющие звенья механизмов, и т. п. Если положения точек механической системы по отношению к данной системе отсчёта определять их декартовыми координатами xk, ук, zk (k = 1,2..., n, где n - число точек системы), то ограничения, налагаемые Связи механические, могут быть выражены в виде равенств (или неравенств), связывающих координаты xk, yk, zk, их первые производные по времени 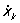 , yk,
, yk, 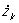 (т. е. скорости точек системы) и время t.
(т. е. скорости точек системы) и время t.
Связи механические, налагающие ограничения только на положения (координаты) точек системы и выражающиеся уравнениями вида
f (..., xk, yk, zk,..., t) = 0, (1)
называются геометрическими. Если же Связи механические налагают ограничения ещё и на скорости точек системы, то они называются кинематическими, а их уравнения имеют вид:
j (..., xk, yk, zk,..., 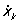 , yk,
, yk, 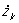 ,..., t) = 0. (2)
,..., t) = 0. (2)
Когда уравнение (2) может быть проинтегрировано по времени, соответствующая кинематическая связь называется интегрируемой и эквивалентна геометрической связи. Геометрические и интегрируемые кинематические связи носят общее название голономных Связи механические (см. Голономные системы). Кинематические неинтегрируемые Связи механические называются неголономными (см. Неголономные системы).
Связи механические, не изменяющиеся со временем, называются стационарными (их уравнения не содержат явно время t), а Связи механические, изменяющиеся со временем, называются нестационарными. Наконец, Связи механические, при которых каждому возможному перемещению точек системы соответствует перемещение прямо противоположное по направлению, называются двусторонними [их уравнения выражаются равенствами вида (1), (2)], а Связи механические, не удовлетворяющие этому условию (например, гибкая нить, допускающая перемещение вдоль нити только в одном направлении), называются односторонними и их уравнения выражаются неравенством вида f (..., xk, yk, zk,...) ³ 0.
Методы решения задач механики существенно зависят от характера Связи механические, налагаемых на систему. Эффект действия Связи механические можно учитывать введением соответствующих сил, называются реакциями связей; при этом для определения реакций (или для их исключения) к уравнениям равновесия или движения системы должны присоединяться уравнения связей вида (1) или (2). Связи механические, для которых сумма элементарных работ всех реакций на любом возможном перемещении системы равна нулю, называются идеальными (например, лишённая трения поверхность или гибкая нить). Для механических систем с идеальными Связи механические можно сразу получить уравнения равновесия или движения, не содержащие реакций связей, используя возможных перемещений принцип, Д"Аламбера - Лагранжа принцип или Лагранжа уравнения.
Лит. см. при статьях Механика и Динамика.
С. М. Тарг.
| "БСЭ" >> "С" >> "СВ" >> "СВЯ" |
Статья про "Связи механические" в Большой Советской Энциклопедии была прочитана 847 раз
| Бургер двойного помола |
| Креветки с газировкой |
TOP 20
- Лемке Михаил Константинович
- Сульфгидрильные группы
- «Казарменный коммунизм»
- Японское море
- Периодическая система элементов
- Глициния
- Башкирская Автономная Советская Социалистическая Республика
- Иммунитет (историч.)
- Андаманское море
- Сенсуализм
- Объединённая партия гаитянских коммунистов
- «Сообразительный»
- Балкано-кавказская раса
- Навигация (морск.)
- Звёздная астрономия
- Ямполь (пос. гор. типа в Донецкой обл.)
- Мандельштама - Бриллюэна рассеяние
- Кульчицкая Елена Львовна
- Театральные учебные заведения
- Электрическая постоянная