


БНБ
"БСЭ" (95279)
- Photogallery
- Естественные науки - Математика - Технология
- Авиация и машиностроение
- Высокие технологии
- Вычислительная техника
- Нанотехнология
- Роботехника
- Энергетика
- Электроника
Преобразование
Определение "Преобразование" в Большой Советской Энциклопедии
Преобразование, одно из основных понятий математики, возникающее при изучении соответствий между классами геометрических объектов, классами функций и т.п. Например, при геометрических исследованиях часто приходится изменять все размеры фигур в одном и том же отношении, увеличивать радиусы кругов на одну и ту же величину, вообще сопоставлять фигурам какого-либо класса другие, получаемые из них по определённым правилам. При решении дифференциальных уравнений операционными методами (см. Операционное исчисление) заменяют данные функции другими, преобразованными функциями, и т.д. Такие соответствия и называются Преобразование Точнее, преобразованием называется соответствие, в силу которого каждому элементу х некоторого множества Х сопоставляется вполне определённый элемент у некоторого другого множества Y. Логически понятие Преобразование совпадает с понятиями функция, отображение, оператор. Термин «Преобразование» чаще употребляют в геометрии и функциональном анализе, при этом обычно считают соответствие между х и у = f (x) взаимно однозначным.
Геометрические преобразования. В геометрии чаще всего рассматриваются точечные Преобразование, при которых каждой точке некоторого многообразия (линии, поверхности, пространства) ставится в соответствие другая точка того же многообразия. Иными словами, точечное Преобразование является отображением многообразия на себя. При точечном Преобразование каждая фигура (прообраз), рассматриваемая как совокупность точек, преобразуется в новую фигуру, называемую образом первоначальной. Если точечное Преобразование взаимно однозначно, то можно определить обратное Преобразование (см. Отображение). Точечное Преобразование называется тождественным, если при нём образ каждой точки совпадает с прообразом. Если ограничиться для определённости точечными Преобразование плоскости, то такие Преобразование могут быть заданы аналитически формулами:
x" = f (х, у), y" = jq (х, у),
где х, у — координаты прообраза, а x’, y" — координаты образа в одной и той же системе координат.
Многие важные классы точечных Преобразование образуют группу, т. е. вместе с любыми двумя Преобразование содержат их произведение (результат последовательного применения), а вместе с каждым Преобразование содержат обратное Преобразование Наиболее важные примеры групп точечных Преобразование плоскости таковы:
1) группа вращений плоскости вокруг начала координат:
x" = х cosa — у sina,
y" = х sina + у cosa,
где a — угол поворота.
2) Группа параллельных переносов, при которых все точки смещаются на один и тот же вектор ai + bj:
x" = х + а, y" = у + b.
3) Группа движений, состоящая из Преобразование, не изменяющих расстояния между точками и ориентации плоскости:
x" = х cosa — у sina + a1,
y" = х sina + у cosa + b1.
См. также Движение в геометрии.
4) Группа движений и зеркальных отражений, состоящая из Преобразование, не изменяющих расстояния между точками плоскости. Совокупность движений и зеркальных отражений, совмещающих некоторую фигуру с собой, называется группой симметрии этой фигуры. Эта группа определяет свойства симметрии фигуры. Например, группа симметрии правильного тетраэдра состоит из 4! = 24 Преобразование, переставляющих между собой его вершины.
5) Группа Преобразование подобия, порождаемая Преобразование движения, зеркального отражения и гомотетии.
6) Группа аффинных Преобразование, состоящая из взаимно однозначных отображений плоскости на себя, при которых прямые переходят в прямые: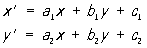 ,
, 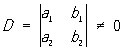
Если c1 = c2, то Преобразование называется центро-аффинным, а если D = 1, то — экви-аффинным; экви-аффинные Преобразование не изменяют площади фигур. См. также Аффинные преобразования.
7) Группа проективных Преобразование, состоящая из взаимно однозначных Преобразование расширенной плоскости (дополненной бесконечно удалённой прямой), при которых прямые линии переходят в прямые: ,
, 
Из этой записи видно, что прямая ах + by + с = 0 переходит при этом Преобразование в бесконечно удалённую прямую. См. также Проективное преобразование.
8) Группа круговых Преобразование (или Преобразование обратными радиусами-векторами), порождаемая Преобразование движения, зеркального отражения, подобия и инверсий. Если точки плоскости изобразить комплексными числами, то Преобразование этой группы запишутся в виде: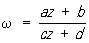 или
или  ,
,
где w = x" + iy’, z = x + iy, 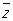 = x - iy. Т. о., они совпадают с дробно-линейными преобразованиями (см. Дробно-линейные функции). Преобразование этой группы обладают круговым свойством, т. е. переводят совокупность прямых и окружностей на плоскости в себя. Они обладают также свойством конформности (см. Конформное отображение). Преобразование плоскости, обладающее круговым свойством, принадлежит всегда группе круговых Преобразование
= x - iy. Т. о., они совпадают с дробно-линейными преобразованиями (см. Дробно-линейные функции). Преобразование этой группы обладают круговым свойством, т. е. переводят совокупность прямых и окружностей на плоскости в себя. Они обладают также свойством конформности (см. Конформное отображение). Преобразование плоскости, обладающее круговым свойством, принадлежит всегда группе круговых Преобразование
Группы 1—7 являются линейными группами, т.к. они переводят прямые линии в прямые. При этом группы 1 и 2 являются подгруппами группы 3, каждая следующая группа (4, 5, 6, 7) содержит в себе предыдущую как часть. Группы 1—6 можно охарактеризовать как совокупность проективных Преобразование, оставляющих неизменным некоторый образ на расширенной плоскости. Например, аффинные Преобразование являются Преобразование, оставляющими на месте бесконечно удалённую прямую. Группа 8 является примером нелинейной группы, т.к. при Преобразование этой группы прямые линии могут перейти в окружности. Преобразование групп 1—8 являются бирациональными преобразованиями, т. е. такими Преобразование, при которых x" и y" рационально выражаются через х и у и обратно.
Наряду с точечными Преобразование, при которых устанавливается соответствие между точками, в геометрии применяются Преобразование фигур, при которых устанавливается соответствие между самими фигурами. Например, в некоторых задачах геометрии заменяют все окружности окружностями же, увеличивая их радиус на определённую величину. Этим определяется Преобразование многообразия окружностей в себя. Рассматриваются также Преобразование, изменяющие природу элементов, т. е. переводящие точки в линии, линии в точки и т.д. Например, можно поставить в соответствие каждой точке М (х, у) прямую ux" + uy" = 1, где u и u — некоторые функции от х и y. Если u и u дробно-линейно зависят от x и y: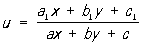 ,
, ,
,
то имеет место общее проективное Преобразование точек плоскости в прямые плоскости. Если при этом b1 = a2, c1 = -a, c2 = -b, то получается полярное Преобразование относительно некоторой линии второго порядка (см. Полюсы и поляры). В частности, когда u = х и u = у, получается полярное Преобразование относительно окружности x2 + y2 = 1. При этом каждой точке на плоскости (х, у) соответствует прямая на плоскости (х’, у"). Кривой Г на плоскости (х, у) соответствует семейство прямых, касающихся некоторой кривой Г’ (или проходящих через одну и ту же точку). Этим устанавливается соответствие между кривыми плоскости (х, у), рассматриваемыми как множество своих точек, и кривыми плоскости (х’, у"), рассматриваемыми как огибающие своих касательных. Более общими являются Преобразование, задаваемые формулой F (x, y, x’, y") = 0. Если задать x и y, то эта формула определяет некоторую кривую на плоскости (х’, у"), а если задать x" и y’, то определяется кривая на плоскости (х, у). Этим устанавливается соответствие точек одной плоскости двухпараметрическому множеству кривых другой плоскости. Указанное соответствие можно распространить до соответствия между кривыми одной плоскости, рассматриваемыми как множество своих точек, и кривыми другой плоскости, рассматриваемыми как огибающие соответствующего семейства кривых. При этом Преобразование касающиеся друг друга кривые одной плоскости переходят в касающиеся друг друга кривые другой плоскости. Поэтому описанные Преобразование называются контактными Преобразование, или П, прикосновения (см. Прикосновения преобразования).
Аналогично Преобразование плоскости определяются Преобразование многомерных (в частности, трёхмерных) пространств. Для каждой из разобранных выше групп Преобразование плоскости имеется трёхмерный аналог, получающийся из неё увеличением числа преобразуемых переменных. Так, группе 1 соответствует группа ортогональных преобразований, группе центро-аффинных Преобразование — группа невырожденных линейных преобразований и т.д. Примером группы Преобразование четырёхмерного пространства является группа Лоренца (см. Лоренца преобразования), играющая важную роль в теории относительности. Преобразование многомерных пространств используются в анализе при вычислении кратных интегралов, так как позволяют свести заданную область интегрирования к более простой области.
Как для групп Преобразование плоскости, так и для групп Преобразование многомерных пространств можно определить понятие близости Преобразование, позволяющее образовать непрерывные группы Преобразование (см. Непрерывная группа).
Для каждой из групп Преобразование существуют свойства фигур, не изменяющиеся при Преобразование соответствующей группы. Эти свойства являются, как говорят, инвариантами относительно данной группы Преобразование Так, при преобразованиях группы движений инвариантно расстояние между двумя точками, при аффинных Преобразование — параллельность прямых, отношение площадей двух фигур, при проективных Преобразование — двойное отношение AB/AD: CB/CD точек A, В, С, D, лежащих на одной прямой. Каждой группе Преобразование соответствует своя область геометрических исследований, изучающая свойства фигур, остающихся инвариантными при Преобразование этой группы (см. Эрлангенская программа). В соответствии с этим различают метрические свойства фигур, аффинные свойства, проективные свойства и т.д. Вообще говоря, чем шире группа, тем теснее связаны эти инвариантные свойства с фигурой. Наиболее общими являются свойства фигур, остающиеся инвариантными при любых топологических Преобразование (т. е. любых взаимно однозначных и непрерывных Преобразование). К ним относятся размерность, связность, ориентируемость (см. Топология).
Особенно важную роль играют Преобразование при установлении новых и при обобщении ранее известных теорем. Если в формулировку некоторой теоремы, доказанной для фигуры F, входят лишь свойства фигуры, инвариантные относительно некоторой группы Преобразование, то теорема сохраняет свою силу для всех фигур, получаемых из F Преобразование этой группы (как говорят, гомологичных или эквивалентных F относительно этой группы). Это свойство Преобразование особенно важно, если среди эквивалентных между собой фигур имеется такая, которая обладает в некоторых отношениях наиболее простыми свойствами. Так, ряд теорем проективной геометрии был установлен впервые для окружности, а потом перенесён на любые невырожденные конические сечения (все невырожденные конические сечения эквивалентны окружности относительно группы проективных Преобразование). При решении геометрических задач на построение часто используют Преобразование, для того чтобы привести фигуры в наиболее удобные для решения положения.
Преобразования функций. Существенное значение имеет также теория групп Преобразование для теории аналитических функций. Там рассматриваются классы функций, не изменяющихся при Преобразование, образующих некоторую группу (см. Автоморфные функции).
Понятие Преобразование играет важную роль и в функциональном анализе, где рассматриваются Преобразование одного множества функций в другое. К таким Преобразование относятся, например, Фурье преобразование, Лапласа преобразование и др. При этих Преобразование каждой функции f ставится по определённому правилу в соответствие другая функция j. Например, преобразование Фурье имеет вид: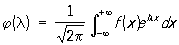 .
.
Оно, как и преобразование Лапласа, относится к классу интегральных Преобразование, определяемых формулами вида: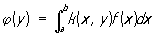 .
.
В ряде случаев Преобразование позволяют заменить операции над функциями более простыми операциями над их образами (например, дифференцирование — умножением на независимую переменную), что облегчает решение уравнений.
Многие уравнения можно записать в виде f = Af, где f — искомая функция, а А — символ Преобразование В этом случае задача решения уравнения может быть истолкована как задача нахождения функции, не изменяющейся при Преобразование Эта точка зрения, называемая принципом неподвижной точки, позволяет в ряде случаев устанавливать существование и единственность решения (см. Сжатых отображений принцип).
Лит.: Ефимов Н. В., Высшая геометрия, 5 изд., М., 1971; Клейн Ф., Высшая геометрия, пер. с нем., М. — Л., 1939; его же, Элементарная математика с точки зрения высшей. Лекции..., пер. с нем., 2 изд., т. 2, М. — Л., 1934; Адамар Ж., Элементарная геометрия, пер. с франц., 4 изд., ч, 1, М., 1957.
| "БСЭ" >> "П" >> "ПР" >> "ПРЕ" >> "ПРЕО" |
Статья про "Преобразование" в Большой Советской Энциклопедии была прочитана 872 раз
| Коптим скумбрию в коробке |
| Семга на горелке |
TOP 20
- Лемке Михаил Константинович
- Сульфгидрильные группы
- «Казарменный коммунизм»
- Японское море
- Периодическая система элементов
- Глициния
- Башкирская Автономная Советская Социалистическая Республика
- Иммунитет (историч.)
- Андаманское море
- Объединённая партия гаитянских коммунистов
- Сенсуализм
- «Сообразительный»
- Балкано-кавказская раса
- Навигация (морск.)
- Звёздная астрономия
- Ямполь (пос. гор. типа в Донецкой обл.)
- Мандельштама - Бриллюэна рассеяние
- Кульчицкая Елена Львовна
- Театральные учебные заведения
- Электрическая постоянная